PREPARATION OF ELEMENT PRIMARY SOLUTIONS

Two principal stock solutions comprising 10 ppm each of Cu²⁺ and Pb²⁺ was prepared by drawing 5 mL from a 1000 ppm standard stock solution of the individual metal ions in HNO₃ into a 500 mL volumetric flask with a pipette and diluting to the volume of the flask with deionized water before mixing by inversion. Calibration solutions were then prepared by serial dilution of the respective 10 ppm primary standards. For this purpose, aliquots of 10, 20, 25 and 50 mL respectively were drawn from the individual primary stock solutions and delivered into separate 100 mL volumetric flasks. The solutions were then diluted to volume with deionized water and thoroughly mixed to obtain 1, 2, 2.5 and 5 ppm calibration solutions.

Isothermal Studies

Isotherm studies are mathematical models we used to better understand mechanism and method of distribution of adsorbate uptake between liquid and adsorbent (KNT­) species based on assumption that mainly related to interaction of adsorbate, homogeneity and heterogeneity of adsorbents. Equilibrium analysis of adsorption relationship between the adsorbent (KNT) concentration in effluent and concentration of adsorbate at stipulated conditions was studied using Langmuir (Langmuir, 1916), Freundlich (Freundlich, 1906), Temkin (Temkin, 1940), Redlich – Peterson (Ayawei, 2017) and Sips (Saadi, 2015) isothermal methods.

Various equations below explain the isotherm models in detail. Equation 1.4a-1.4b depicts Langmuir equation and its linearized form with 1.4c showing equation of its dimensionless factor (R_L) respectively.

Equations (1.5a, & b) – (1.6a, & b) are the main and linearized equations of Freundlich and Temkin models correspondingly.

$qe=\frac{QmaxKlCe}{1+KLCe}$ (1.4a)

$\frac{Ce}{qe}=\frac{Ce}{Qmax}+\frac{1}{QmaxKl}$ (1.4b)

$R_L=\frac{1}{1+K_L{C}_e}$ (1.4c)

$q_e=K_f{C}_e^{1/nf}$ (1.5a)

$Log{q}_e=\frac{1}{n}\log C_e+\log K_f$ (1.5b)

$q_e=\frac{RT}{b}\left(\ln K{C}_e\right)$ (1.6a)

$q_e=B\ln A+B\ln C_e$ (1.6b)

Where $B=\frac{RT}{b}$ (1.6c)

$\ln (K_R\frac{C_e}{q_e}-1=b_R\ln (C_e)+\ln (a_g)$ (1.7)

$K_s\ln \left(C_e\right)=-\ln \left(\frac{K_s}{q_e}\right)+\ln \left(n_s\right)$ (1.8)

Ce is concentration obtained at equilibrium in mg/L, qe is the amount of Pb²⁺ and Cu²⁺ taken onto the adsorbent surface at equilibrium (mg/g), qmax is the Langmuir maximum monolayer adsorption capacity of adsorbent expressed in mg/g and KL is the Langmuir constant of adsorption calculated in L/mg. and n are Freundlich constants which incorporates the factors affecting the adsorption capacity and adsorption intensity respectively. A is Temkin isotherm constant (L/g), from the value of Temkin constant B, a constant b (J/mol) related to the heat of absorption can be obtained with the relation B=RT/b, T is the temperature expressed in (K), R is the general gas constant (8.314 J/mol K). Where, Redlich – Peterson parameters in equation (1.7) KR/aR=KF and (1-β) = 1/n of Freundlich isotherm model. It reduces to Langmuir equation when β=1, aR=b (Langmuir adsorption constant), and KR=bQ˳, and it reduces to Henry’s equation when β=0 and Henry’s constant is represented by 1/(1+b) in Redlich – Peterson model.

Thermodynamic Adsorption Studies

To study the feasibility of adsorption processes, the thermodynamic parameters, such as Gibbs free energy ΔG^o, enthalpy ΔH^o, and entropy ΔS^o changes can be estimated from the following equations (Kumar, 2011).

$∆G°=-RT\ln K_c$ (1.7)

$\ln K_c=\frac{∆S}{R}-\frac{∆H}{RT}$ (1.8)

$K_c=\frac{q_e}{C_e}$ (1.9a)

where R is the gas constant, T is the temperature in Kelvin and Van ‘t Hoff enthalpic can be obtained from qe/Ce. ∆H^o and ∆S^o can be obtained from the plot of ln versus 1/T.).

The activation energy E_a for the adsorption was determined using the Arrhenius equation below:

$\ln K_1=\ln A-\ln \frac{E_a}{RT}$ (1.9b)

where k ₁ is the biosorption rate constant, A is the Arrhenius constant, E_a is the activation energy (kJ mol⁻¹), R is the gas constant (8.314 J mol⁻¹ K⁻¹), and T is the temperature (K).

Kinetics Model

Kinetics were studied using the pseudo-first-order, otherwise called Lagergren (Lagergren, 1898), (Qureshi, 2020), pseudo-second-order (Ys & Mckay, 1999), (Tang, Ran, Li, Zhang, & Xiang, 2020), Elovich (Ayawei, 2017) , Avrami (Rojas, Suarez, Moreno, Silva-Agredo, & Torres-Palma, 2019), (Weber & Morris, 1963), kinetic models. The equations (8) – (14) below represents respective form of their linear equations. $Log(q_e-q_t)=Log{q}_e-\frac{K_{1}t}{2.303}$ (1.10)

$\frac{1}{q_t}=\frac{1}{K_2{q}_e^2}+\frac{t}{q_e}$ (1.11)

$\ln \frac{q_e}{C_e}=\ln K_e{q}_m-\frac{q_e}{q_m}$ (1.12)

$\frac{1}{ln[1-Y(t\left)\right]}=\ln K-n\ln t$ (1.13)

$q_e=K_{diff}{t}^{1/2}+l$ (1.14)

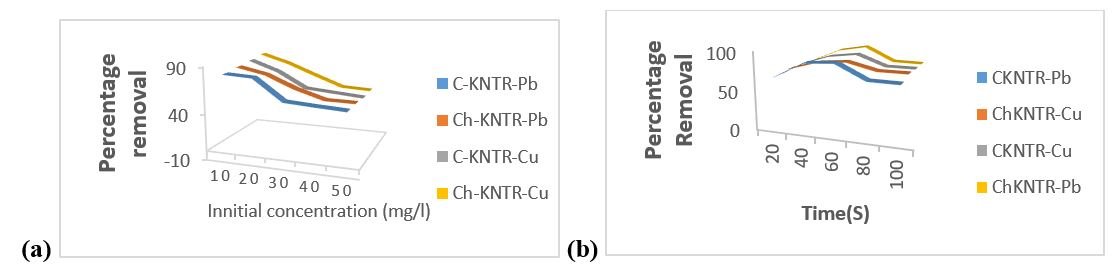
Effect of Initial Concentration on Percentage Adsorption

Degree of adsorption is a function of adsorbent initial concentration as shown from the findings on examined varying concentrations data of Pb²⁺ and Cu²⁺ ions depicted in figure 3.1(a) below. The effect of varying Pb²⁺ and Cu²⁺ ion concentration is highly important because it will aid insight in C-KNTR and Ch-KNTR effectiveness during industrial large-scale production and applications. The result showed that adsorption efficacy of C-KNTR and Ch-KNTR decreased with increase in initial concentration of both Pb²⁺ and Cu²⁺ ions from 10-50 mg/L. The decrease in adsorption percentage is due to saturation of available limited number of active sites on adsorbent as heavy metals concentration increases (Chaudhary, et al., 2019; Oluwasola, et al., 2019). The highest optimum adsorption occurred at 10 mg/L concentration with adsorption percentage of (81.267 % for C-KNTR-Pb²⁺, 83.258 % for Ch-KNTR-Pb²⁺) and (85.369 % for C-KNTR-Cu²⁺ and 87.879 % for Ch-KNTR-Cu²⁺) respectively.

Effect of Contact Time

Figure 3.1(b) below illustrates result of the effect contact time exerted on the percentage of Pb²⁺ and Cu²⁺ removal by C-KNTR and Ch-KNTR studied. Adsorption efficiency of metals studied was quick at the beginning of contact time due to increased surface area and presence of copious adsorptive reactive sites present on the adsorbent and then followed a slow but steady increase of adsorption with time until equilibrium was attained at 60 min, beyond which there was noticeable significant decrease in the adsorption with contact time until 80 min, after which there was no significant increase or decrease of adsorption rate with time (Khalek, 2019), (Thakur, 2020). The percentage adsorption at 60 min agitation are (89.982 % for C-KNTR-Pb²⁺, 90.909 % for Ch-KNTR-Pb) and (86.782 % for C-KNTR-Cu²⁺ and 83.973 % for Ch-KNTR-Cu²⁺) respectively.

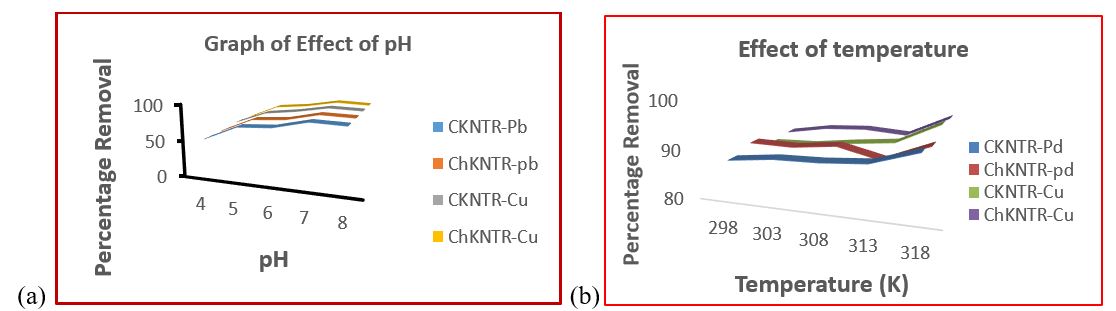
Effect of pH

The ionization and chemistry of surface adsorption properties on adsorbent material are mostly influenced by hydronium ion concentration (pH) of the solution by interfering with the charges present on the reactive sites. Figure 3.2a show the graph effect of pH on adsorptive properties of C-KNTR and Ch-KNTR. The surface nature of a C-KNTR and Ch-KNTR studied depends not only on the functional groups but also on the isoelectric point of zero charge (pH _PZC, ) (Gümüş, 2019); (Das, Das, Bhowal, & Bhattachariee, 2020). At a lower pH (acidic pH 4), the external surface charges on C-KNTR and Ch-KNTR are highly protonated, these ions compete with Pb²⁺ and Cu²⁺ ions for accessible adsorption reactive sites. Thus, low adsorption of Pb²⁺ and Cu²⁺ ions on C-KNTR and Ch-KNTR took place at pH4 value. The high C-KNTR and Ch-KNTR adsorption observed was due to more negatively charged present on adsorbent surface as pH value increased from pH4-pH7 thereby increasing the adsorption efficiency of Pb²⁺ and Cu²⁺ ions due to decrease in protonation on the adsorbent caused by exchange of hydroxonium ions with hydroxyl ions (Das et al., 2020). The C-KNTR and Ch-KNTR studied adsorption efficiency from the result improved with increase in pH from pH4 until it attains optimum at pH7 with removal percentage of (85.606 % of CKNTR-Pb²⁺ and 85.507 % of ChKNTR-Pb²⁺) and (85.886% of CKNTR-Cu²⁺ and 86.059 % of ChKNTR-Cu²⁺) respectively. Low adsorption observed at higher pH above pH7 will be attributed to inhibited adsorptive sites on C-KNTR and Ch-KNTR caused by precipitation due to formation of complexes between reactive sites on the adsorbent and Pb²⁺ and Cu²⁺ ions.

Effect of Temperature

The result of temperature effect on C-KNTR and Ch-KNTR in figure 3.2 (b) below suggest that adsorption efficiency of both Pb²⁺ and Cu²⁺ on C-KNTR and Ch-KNTR was significantly high as temperature increased from 298 to 318 K. The obtained result could be attributed to both increase in kinetic energy of Pb²⁺ and Cu²⁺ ions and C-KNTR with Ch-KNTR pore size enlargement which ultimately increases the surface area and efficiency of adsorption sites present on the adsorbent suggesting that Pb²⁺ and Cu²⁺ adsorption is an endothermic process. Quantity of Pb²⁺ and Cu²⁺ adsorbed on C-KNTR and Ch-KNTR at 318 K maximum temperature studied are (92.7152 % of CKNTR-Pb²⁺ and 91.519 % of ChKNTR-Pb²⁺) and (93.702 % of CKNTR-Cu²⁺ and 93.079 % of ChKNTR-Cu²⁺) correspondingly.

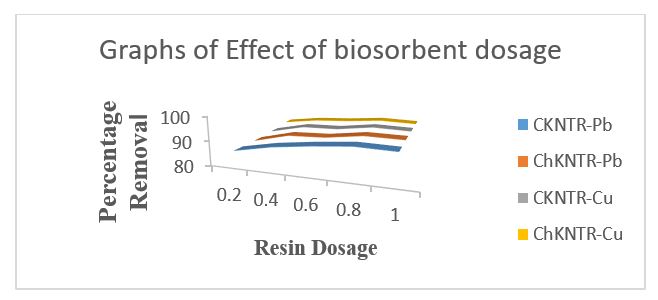
Effect of Adsorption Dosage

The result from figure 3.3 below show that Pb²⁺ and Cu²⁺ adsorption efficiency increased with C-KNTR and Ch-KNTR dosage from 0.2 to 1 g with maximum percentage removal at 1 g as (92.061 % for C-KNTR-Pb²⁺, 92.154 % for Ch-KNTR-Pb²⁺) and (92.188 % for C-KNTR-Cu²⁺, 93.059 % for Ch-KNTR-Cu²⁺) respectively due to availability of more active sites. However, adsorption capacity reduced from 14.294 to 4.298 mg/g for C-NKTR- Pb²⁺, 14.113 to 4.114 mg/g for C-NKTR- Cu²⁺ and 13.394 to 4.291 mg/g for Ch-NKTR-Pb²⁺, 12.103 to 3.817 mg/g for Ch-NKTR-Cu²⁺ at 1 g dosage. The decrease in adsorption capacity per unit mass of C-KNTR and Ch-KNTR observed may be due to decrease in total surface area, resulting from overlap or accumulation of adsorption sites in line with (Shen, 2020)report.

Thermodynamic Modeling

Thermodynamic parameters such as standard Gibb’s free energy change (∆ G^o ), standard enthalpy change (∆ H^o ), and standard entropy change (∆ S^o ) was studied for insight in the feasibility of CKNTR-Pb²⁺, CKNTR-Cu²⁺ and ChKNTR-Pb²⁺, ChKNTR-Cu²⁺ biosorption process and the result from Arrhenius equation above presented in table 3.5 below also show the activation energies of the sorption process. From table 3.2, positive value of ∆H^o> 0 suggest that adsorption was endothermic in nature and also reaffirm that the mechanism of adsorption is physisorption. This reaffirmation indicates that bond between CKNTR-Pb²⁺, CKNTR-Cu²⁺ and ChKNTR-Pb²⁺, ChKNTR-Cu²⁺ is van der Waals interactions caused by increase degree of freedom at solid liquid interface throughout the adsorption process. The negative value of ∆G^o (kJ/mol) in the obtained result increased with temperature suggest that high temperature favors the adsorption process. Hence, spontaneity of all the studied adsorption process. Positive ∆S ^o (kJ/mol) in table 3.5 suggest that the degree of freedom (randomness) increased at the solid-liquid interface during CKNTR-Pb²⁺, CKNTR-Cu²⁺ and ChKNTR-Pb²⁺, ChKNTR-Cu²⁺ and reversible adsorption process. The activation energy (Ea) can give an idea about the rate and type of adsorption. Physisorption usually have activation energies (Ea) in the range of 5 to 40 kJ/mol, while higher activation energies (Ea) of 40 to 800 kJ/mol suggest chemisorption. The positive value of obtained result in table 3.5 show that the activation energies (Ea) was less than 40 kJ/mol which further reaffirm that physisorption is the mechanism of CKNTR-Pb²⁺, CKNTR-Cu²⁺ and ChKNTR-Pb²⁺, ChKNTR-Cu²⁺ adsorption process.